Power functions and fitting them
- Surface forces - fluids, adhesion - are the dominating forces in the lives of bugs, while gravity dominates the lives of elephants. This is because the ratio of surface area to volume depends on scale; ie, a bug has a bigger skin to meat ratio.
- Find the relationship between the ratio Surface Area / Volume and the edge length of a cube, ie find the function \( SA / V = f(x) \) where x is edge length.
- Do the same with the radius of a sphere.
- Suppose an elephant is 1000 times the length of a beetle. What is the ratio of their SA / V ratios?
- Extra point: name a 3D shape that has a different relationship between this ratio and its linear dimensions.
- The scattering of light in the atmosphere obeys the relationship \( I = a\lambda^{-1/4} \), where I is the amount of scattering and \( \lambda \) is the light wavelength.
- The acronym ROYGBIV for the rainbow is in order of decreasing wavelength. Sketch the shape of the above function of scattering amount on the y axis vs. wavelength on the x axis. Explain why this means blue light is scattered more, and red light less. (This is why the sky is blue and the sun yellow).
- If color A has double the wavelength of color B, what is the ratio of their scattering amounts?
- If color A is scattered twice as much as color B, what is the ratio of their wavelengths?
- Isolate y in the following equation, ie write it in the form \( (1) \) :
\( 4yx^2 = \frac{x^{-3}}{4} \) - Fitting a power function to data means finding the values of a and b for which the fit is closest. A neat trick to transform our curves to familiar linear curves makes use of the fact that \( \log{ab} = \log{a} + \log{b} \) .
- Show why \( \log{y} \) vs. \( \log{x} \) is linear when \( y = f(x) \) is a power function. (Recall that \( \log{x^b} = b\log{x} \) ).
- Express the constants a and b in terms of the linear function found in part 1.
- A straight line fit to data on a log-log plot (the log of y values vs the log of x values) has a slope of 2 and a y intercept of -1. What is the power function relationship of this data?
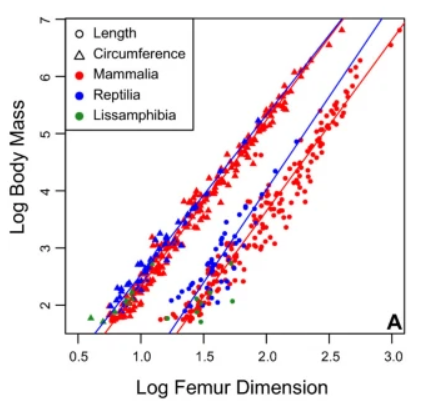
- Estimate the values a and b of the power relationship between the body mass and femur circumference of mammals using this chart from [1].
This assigment deals with relationships of the form
\( \label{eq:power} \begin{equation} y = ax^b \end{equation} \)
where a and b are real constants, and x and y are real variables. This differs from a polynomial equation in that the exponent b need not be a natural number, and in that x only appears once.